拓扑排序和二分图

发表于 更新于 本文字数： 1.2k 阅读时长 ≈ 5 分钟

1 拓扑排序（有向图）

课程表Ⅱ

1.1 BFS（易理解）

创建一个表示入度的数组，初始将入度为0的节点加入队列，后续依次弹出队列，每次弹出node，减小node指向的节点的入度，入度为0的加入队列，直到队列为空，结果需要判定出队列的节点数和图的总节点数相同，不同则代表有循环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> g(numCourses);
        vector<int> inDegree(numCourses);
        for (auto& e : prerequisites) {
            g[e[1]].push_back(e[0]);
            ++inDegree[e[0]];
        }
        queue<int> q;
        vector<int> ret;
        for (int i = 0; i < numCourses; ++i)
            if (inDegree[i] == 0) q.push(i);
        while (!q.empty()) {
            int node = q.front(); q.pop();
            ret.push_back(node);
            for (auto e : g[node]) {
                --inDegree[e];
                if (inDegree[e] == 0)
                    q.push(e);
            }
        }
        return ret.size() == numCourses ? ret : vector<int>();
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class Solution {
    public int[] FindOrder(int numCourses, int[][] prerequisites) {
        List<List<int>> graph = Enumerable.Range(0, numCourses).Select(_ => new List<int>()).ToList();
        int[] inDegress = new int[numCourses];
        foreach (var pair in prerequisites) {
            graph[pair[1]].Add(pair[0]);
            ++inDegress[pair[0]];
        }
        Queue<int> queue = new();
        List<int> result = new();
        for (int node = 0; node < numCourses; ++node)
            if (inDegress[node] == 0) queue.Enqueue(node);
        while (queue.Count > 0) {
            int node = queue.Dequeue();
            result.Add(node);
            foreach (var outNode in graph[node]) {
                --inDegress[outNode];
                if (inDegress[outNode] == 0)
                    queue.Enqueue(outNode);
            }
        }
        return result.Count() == numCourses ? result.ToArray() : Array.Empty<int>();
    }
}

1.2 DFS（递归）

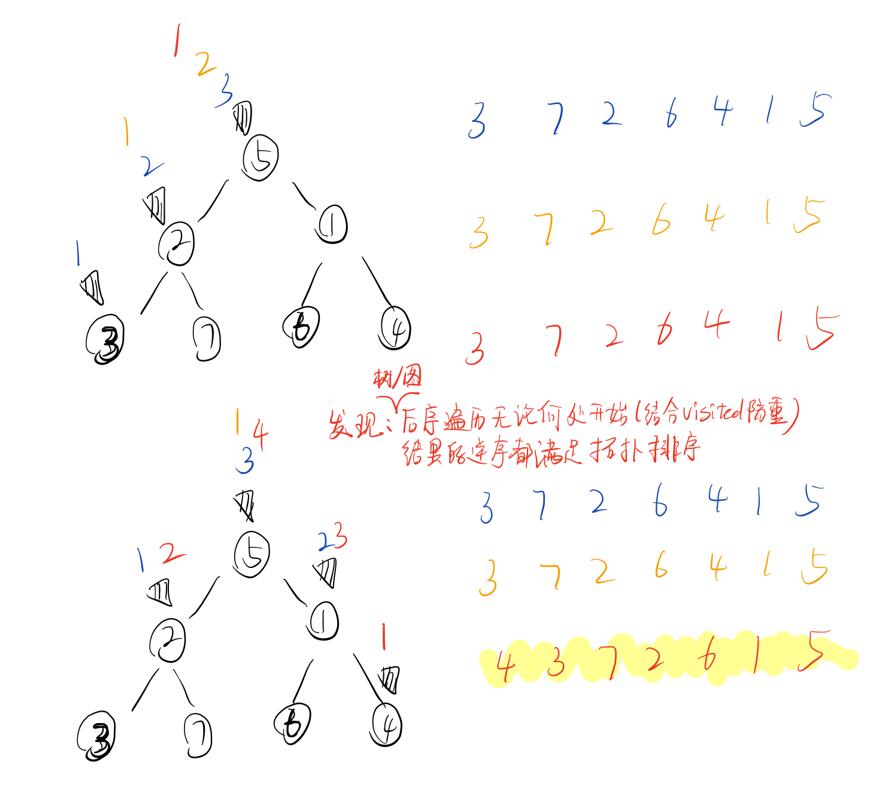
后序遍历的结果进行反转，就是拓扑排序的结果

[2025/11/22]下面的图看起来很像二叉树，其实是图，并且有向图的方向是向上的，看的话应该倒过来，因此代码输出的结果第一个是5，所以最后需要反序一下！

后序遍历与拓扑排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// visited防止重复处理节点
// used用来判断成环
class Solution {
public:
    vector<bool> visited; // 不重置
    vector<bool> used; // 每次递归，回溯重置
    vector<int> postOrder; // 结果数组

    // 判断有环，顺便记录下后序遍历的节点
    bool isCircle(vector<vector<int>>& g, int node) {
        if (used[node]) return true;
        if (visited[node]) return false;
        visited[node] = true;
        used[node] = true;
        for (auto e : g[node])
            if (isCircle(g, e)) return true; // 有环直接返回
        postOrder.push_back(node); // 后序遍历位置（递归后面）
        used[node] = false;
        return false;
    }

    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> g(numCourses);
        for (auto& e : prerequisites) g[e[1]].push_back(e[0]);
        visited.resize(numCourses, false);
        used.resize(numCourses, false);
        for (int i = 0; i < numCourses; ++i)
            if (isCircle(g, i)) return vector<int>(); // 有环直接返回
        reverse(postOrder.begin(), postOrder.end()); // 最后反序很重要
        return postOrder;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class Solution {
    private static bool HasCircle(HashSet<int> visited, HashSet<int> used, List<List<int>> graph, int node, List<int> ret) {
        if (used.Contains(node)) return true;
        if (visited.Contains(node)) return false;
        visited.Add(node);
        used.Add(node);
        foreach (var outNode in graph[node])
            if (HasCircle(visited, used,graph, outNode, ret)) return true;
        ret.Add(node);
        used.Remove(node);
        return false;
    }

    public int[] FindOrder(int numCourses, int[][] prerequisites) {
        List<List<int>> graph = Enumerable.Range(0, numCourses).Select(_ => new List<int>()).ToList();
        int[] inDegress = new int[numCourses];
        foreach (var pair in prerequisites)
            graph[pair[1]].Add(pair[0]);
        HashSet<int> visited = new();
        HashSet<int> used = new();
        List<int> ret = new();
        for (int i = 0; i < numCourses; ++i)
            if (HasCircle(visited, used, graph, i, ret)) return Array.Empty<int>();
        return Enumerable.Reverse(ret).ToArray();
    }
}

2 二分图（无向图）

图的节点只有两种颜色：红和蓝，相同颜色不能相邻，判断是否是二分图，可有两种方法：DFS和BFS

可能的二分法

2.1 DFS

注意visited不要重置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    vector<bool> visited;
    vector<bool> color;
    bool core(vector<vector<int>>& g, int node) {
        visited[node] = true;
        for (auto e : g[node]) {
            if (!visited[e]) {
                color[e] = !color[node];
                if (core(g, e) == false)
                    return false;
            }
            else {
                if (color[e] == color[node])
                    return false;
            }
        }
        return true;
    }

    bool possibleBipartition(int n, vector<vector<int>>& dislikes) {
        vector<vector<int>> g(n + 1);
        for (auto& e : dislikes) {
            g[e[0]].push_back(e[1]);
            g[e[1]].push_back(e[0]);
        }
        visited.resize(n + 1, false);
        color.resize(n + 1, false);
        for (int i = 1; i <= n; ++i) {
            if (visited[i]) continue;
            if (core(g, i) == false) return false;
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public class Solution
{
    public bool PossibleBipartition(int n, int[][] dislikes)
    {
        List<List<int>> graph = Enumerable.Range(0, n).Select(_ => new List<int>()).ToList();
        foreach (var pair in dislikes)
        {
            graph[pair[1] - 1].Add(pair[0] - 1);
            graph[pair[0] - 1].Add(pair[1] - 1);
        }
        bool[] color = new bool[n];
        bool[] visited = new bool[n];
        for (int i = 0; i < n; ++ i)
        {
            if (visited[i]) continue;
            if (!DFS(graph, color, visited, i))
                return false;
        }
        return true;
    }

    private bool DFS(List<List<int>> graph, bool[] color, bool[] visited, int node)
    {
        visited[node] = true;
        foreach (var neighbor in graph[node])
        {
            if (visited[neighbor])
            {
                if (color[neighbor] == color[node])
                    return false;
            }
            else
            {
                color[neighbor] = !color[node];
                if (!DFS(graph, color, visited, neighbor))
                    return false;
            }
        }
        return true;
    }
}

2.2 BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    vector<bool> visited;
    vector<bool> color;
    bool core(vector<vector<int>>& g, int node) {
        queue<int> q;
        q.push(node);
        while (!q.empty()) {
            int cur = q.front(); q.pop();
            visited[cur] = true;
            for (auto e : g[cur]) {
                if (!visited[e]) {
                    color[e] = !color[cur];
                    q.push(e);
                }
                else {
                    if (color[e] == color[cur])
                        return false;
                }
            }
        }
        return true;
    }

    bool possibleBipartition(int n, vector<vector<int>>& dislikes) {
        vector<vector<int>> g(n + 1);
        for (auto& e : dislikes) {
            g[e[0]].push_back(e[1]);
            g[e[1]].push_back(e[0]);
        }
        visited.resize(n + 1, false);
        color.resize(n + 1, false);
        for (int i = 1; i <= n; ++i) {
            if (visited[i]) continue;
            if (core(g, i) == false) return false;
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
public class Solution
{
    public bool PossibleBipartition(int n, int[][] dislikes)
    {
        List<List<int>> graph = Enumerable.Range(0, n).Select(_ => new List<int>()).ToList();
        foreach (var pair in dislikes)
        {
            graph[pair[1] - 1].Add(pair[0] - 1);
            graph[pair[0] - 1].Add(pair[1] - 1);
        }
        Queue<int> queue = new();
        bool[] color = new bool[n];
        bool[] visited = new bool[n];
        for (int i = 0; i < n; ++ i)
        {
            if (visited[i]) continue;
            queue.Clear();
            queue.Enqueue(i);
            if (!BFS(graph, queue, color, visited))
                return false;
        }
        return true;
    }

    private bool BFS(List<List<int>> graph, Queue<int> queue, bool[] color, bool[] visited)
    {
        while (queue.Count > 0)
        {
            var curNode = queue.Dequeue();
            visited[curNode] = true;
            foreach (var neighbor in graph[curNode])
            {
                if (visited[neighbor])
                {
                    if (color[neighbor] == color[curNode])
                        return false;
                }
                else
                {
                    color[neighbor] = !color[curNode];
                    queue.Enqueue(neighbor);
                }
            }
        }
        return true;
    }
}

参考

  1. 二分图判定算法
  2. 环检测及拓扑排序算法