Lizq的个人博客

发表于 本文字数： 1.1k 阅读时长 ≈ 4 分钟

Qt的信号与槽机制是如何实现的？

猜测1：回调函数

  • 这里用C11出现的function来封装所有可调用的对象：函数、指针、lambda、bind创建的对象、重载了小括号的仿函数
  • 通过unordered_multimap来记录某个字符串与一个可调用对象的映射（注意unordered_multimap未实现[]和at函数，不能通过这类方式获取value）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
class Connection {
	unordered_multimap<string, function<void()>> mmap;
public:
	// 按照名称建立映射关系
	void connect(const string& name, const function<void()>& callback) {
		//mmap[name] = callback; ERROR
		mmap.insert({ name, callback });
	}
	void invok(const string& name) {
		auto res = mmap.equal_range(name);
		auto l = res.first, r = res.second;
		while (l != r) {
			l->second();
			++l;
		}
	}
};

// 全局共享的Connection
static Connection con;

class Tom {
public:
	void miaow() {
		cout << "喵" << endl;
		con.invok("mouse");
	}
};

class Jerry {
public:
	Jerry() {
		// 普通类函数的第一个参数是this，所以这里绑定this
		con.connect("mouse", bind(&Jerry::RunAway, this));
	}
	void RunAway() {
		cout << "那只笨又猫来了，快跑！" << endl;
	}
};

int main() {
	// 模拟嵌套层级很深的场景，外部不能直接访问到tom
	struct A {
		struct B {
			struct C {
			private:
				Tom tom;
			public:
				void MiaoMiaoMiao() {
					tom.miaow();
				}
			} c;
			void MiaoMiao() {
				c.MiaoMiaoMiao();
			}
		} b;
		void Miao() {
			b.MiaoMiao();
		}
	} a;

	// 模拟嵌套层级很深的场景，外部不能直接访问到jerry
	struct D {
		struct E {
			struct F {
			private:
				Jerry jerry1, jerry2, jerry3;
			} f;
		} e;
	} d;

	a.Miao();
}

输出结果：

阅读全文 »

发表于 更新于 本文字数： 1.2k 阅读时长 ≈ 5 分钟

1 拓扑排序（有向图）

课程表Ⅱ

1.1 BFS（易理解）

创建一个表示入度的数组，初始将入度为0的节点加入队列，后续依次弹出队列，每次弹出node，减小node指向的节点的入度，入度为0的加入队列，直到队列为空，结果需要判定出队列的节点数和图的总节点数相同，不同则代表有循环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> g(numCourses);
        vector<int> inDegree(numCourses);
        for (auto& e : prerequisites) {
            g[e[1]].push_back(e[0]);
            ++inDegree[e[0]];
        }
        queue<int> q;
        vector<int> ret;
        for (int i = 0; i < numCourses; ++i)
            if (inDegree[i] == 0) q.push(i);
        while (!q.empty()) {
            int node = q.front(); q.pop();
            ret.push_back(node);
            for (auto e : g[node]) {
                --inDegree[e];
                if (inDegree[e] == 0)
                    q.push(e);
            }
        }
        return ret.size() == numCourses ? ret : vector<int>();
    }
};
阅读全文 »

发表于 更新于 本文字数： 919 阅读时长 ≈ 3 分钟

带限制的最短路

错误示例（Dijkstra）

全局的dist记录着最短距离，但它并未记录是几跳获得的。例如，到达终点的前一跳，从X->dst，我的代码中只限制了到达X最多k+1跳，此时更新了dist[X]，当更新到dst时，利用的dist[X]是经过k跳的X作为跳板，则结果是经过了k+2跳，超出了限制，因此结果必然是错误的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Item {
public:
    int node, skip, dis;
    Item(int a, int b, int c):node(a),skip(b),dis(c){}
    bool operator>(const Item& R) const {
        return this->dis > R.dis;
    }
};
class Solution {
public:
    int INF = 0x3f3f3f3f;
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        vector<vector<pair<int, int>>> g(n);
        for (auto& e : flights) g[e[0]].push_back({ e[1], e[2] });
        vector<int> dist(n, INF);
        dist[src] = 0;
        priority_queue<Item, vector<Item>, greater<Item>> pq;
        pq.emplace(src, 0, 0);
        while (!pq.empty()) {
            auto cur = pq.top(); pq.pop();
            int node = cur.node;
            int dis = cur.dis;
            int skip = cur.skip;
            if (skip > k) continue;
            for (auto& e : g[node]) {
                int w_node = e.first;
                int w_weight = e.second;
                if (dist[w_node] > dist[node] + w_weight) {
                    dist[w_node] = dist[node] + w_weight;
                    pq.emplace(w_node, skip + 1, dist[w_node]);
                }
            }
        }
        return dist[dst];
    }
};

再次尝试Dijkstra（完全没必要）

阅读全文 »

发表于 更新于 本文字数： 968 阅读时长 ≈ 4 分钟

逆序对计算

1 归并排序

归并排序天然就可统计逆序对，在归并时有以下两种方式统计：

当左侧当前指针指向位置的数字CUR较小时，本轮将其加入归并后的数组，注意到右数组当前指针左边的都是小于CUR的，但是他们位置却在其右侧，所以逆序对贡献为l2-old_l2

1
2
3
4
5
6
if (a <= b) { // 这里包含等于 可以用全1数组模拟想想
    trr[p++] = arr[l1++];
    ret += (l2-old_l2);
}
else 
    trr[p++] = arr[l2++];
阅读全文 »

发表于 更新于 本文字数： 1.1k 阅读时长 ≈ 4 分钟

需求

  • 数组区间内经常发生修改，但是又要频繁求得区间的各类统计信息例如最大值、最小值、区间和等等。
  • 对于一个数组频繁求区间和和修改的情况下：
    • 普通操作：修改：O(1)；区间和：O(n)
    • 前缀和：修改：O(n)；区间和：O(1)
    • 线段树：修改：O(nlogn)；区间和：O(nlogn)

线段树

  • 将数组以二分的形式建成一棵二叉树，叶子节点为数组的值，非叶子节点保存相应的统计信息。这棵树近似完全二叉树的结构，所以可以用数组来构建
  • 下面所列举的代码只需要改变给tree[node]赋值相关代码即可实现求最大值、最小值、区间和，肥肠方便
  • 307. 区域和检索 - 数组可修改

1、数组版

阅读全文 »

发表于 更新于 本文字数： 656 阅读时长 ≈ 2 分钟

需求

  • 随机修改数组中一个数字
  • 求前缀和
  • 以上操作需要频繁操作

预备知识：lowbit

lowbit指数字的二进制最低位1及后续0取出后的数字

1
2
3
int lowbit(int a){
    return a & -a;
}
阅读全文 »

发表于 更新于 本文字数： 455 阅读时长 ≈ 2 分钟

const要点

  • C的const是虚假的，就是个只读量，只是说不能通过变量名进行修改，但是拿到指针就可修改；
  • C++的const会保险一些，会有类似符号表的东西；但是类内的const普通成员变量则依旧会被通过指针改变
  • 静态const和全局const虽然可以通过指针修改，编译时期可能不会报错，但是运行到那个地方就会报错
  • const只在编译期间保证常量被使用时的不变性，无法保证运行期间的行为。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class A {
public:
    const int val2 = 22;
    static int val3;
    static const int val4 = 44; // !
};
int A::val3 = 33;
const int val5 = 55;
int val6 = 66;
int main() {
    const int val1 = 11;
    int* p1 = (int*)&val1; // 栈区，拿到地址随便改，但是符号表会覆盖
    *p1 = 1111;
    cout << &val1 << " " << val1 << endl;
    cout << p1 << " " << *p1 << endl;
    cout << "===" << endl;

    A ins;
    int* p2 = (int*)&ins.val2;
    *p2 = 2222; // 栈区，拿到地址随便改
    cout << &ins.val2 << " " << ins.val2 << endl;
    cout << p2 << " " << *p2 << endl;
    cout << "===" << endl;

    int* p3 = (int*)&A::val3;
    *p3 = 3333; // 全局数据区，但是不在常量区，可以修改
    cout << p3 << " " << *p3 << endl;
    cout << &A::val3 << " " << A::val3 << endl;
    cout << "===" << endl;

    int* p4 = (int*)&A::val4;
    //*p4 = 4444; // 编译不出错，运行会异常（常量区不能修改）
    cout << p4 << " " << *p4 << endl;
    cout << &A::val4 << " " << A::val4 << endl;
    cout << "===" << endl;

    int* p5 = (int*)&val5;
    //*p5 = 5555; // 编译不出错，运行会异常（常量区不能修改）
    cout << p5 << " " << *p5 << endl;
    cout << &val5 << " " << val5 << endl;
    cout << "===" << endl;

    int* p6 = (int*)&val6;
    *p6 = 6666; // 全局数据区，但是不在常量区，可以修改
    cout << p6 << " " << *p6 << endl;
    cout << &val6 << " " << val6 << endl;
    return 0;
}

输出结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/*
00EFFD98 11
00EFFD98 1111
===
00EFFD80 2222
00EFFD80 2222
===
0027C038 3333
0027C038 3333
===
00279B38 44
00279B38 44
===
00279B30 55
00279B30 55
===
0027C03C 6666
0027C03C 6666
*/
阅读全文 »

发表于 更新于 本文字数： 1.1k 阅读时长 ≈ 4 分钟

1 状态模式

  • 在软件构建过程中，某些对象的状态如果改变，其行为也会随之改变，比如文档处于只读状态，其支持的行为和读写状态支持的行为可能完全不同
  • 允许一个对象在其内部状态改变时改变它的行为。从而使对象看起来似乎修改了其行为
  • 用类表示状态，通过切换类改变对象状态
  • 跟Strategy模式很像，区别是：状态模式采用单例模式，抽象类包含指向下一个状态的指针

2 问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
enum NetworkState{
    Network_Open,
    Network_Close,
    Network_Connect
    // 假设未来有新状态：Network_Wait，怎么办？
};

class NetworkProcessor{
    NetworkState state;

public:
    void Operation1(){
        if (state == Network_Open){
            //**********
            state = Network_Close;
        }
        else if (state == Network_Close){
            //..........
            state = Network_Connect;
        }
        else if (state == Network_Connect){
            //$$$$$$$$$$
            state = Network_Open;
        }
    }

    void Operation2(){
        if (state == Network_Open){
            //**********
            state = Network_Connect;
        }
        else if (state == Network_Close){
            //..........
            state = Network_Open;
        }
        else if (state == Network_Connect){
            //$$$$$$$$$$
            state = Network_Close;
        }
    }

    void Operation3(){
        // ...
    }
};

3 状态v1

阅读全文 »

发表于 更新于 本文字数： 740 阅读时长 ≈ 3 分钟

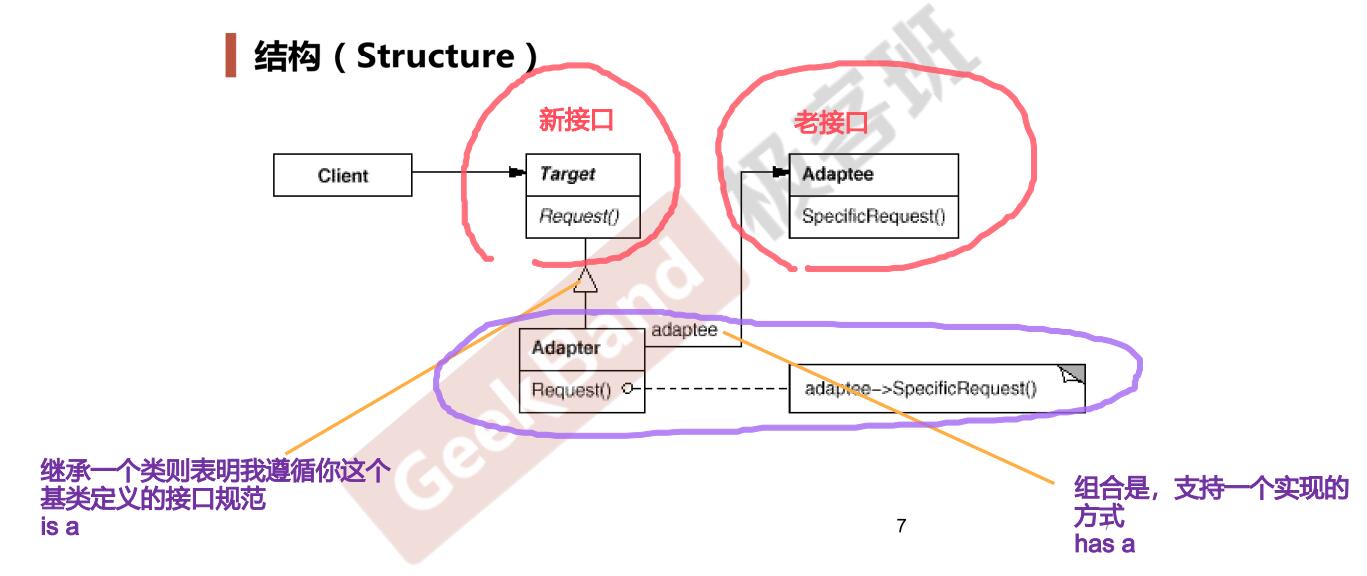
1 适配器模式

  • 在软件系统中，由于应用环境的变化，常常需要将“一些现存的对象”放在新的环境中应用，但是新环境要求的接口是这些现存对象所不满足的。
  • 将一个类的接口转换成客户希望的另一个接口，Adapter模式使得原本由于接口不兼容而不能一起工作的那些类可以一起工作

2 适配器v1

适配器模式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
// 目标接口（新接口）
class ITarget{
public:
    virtual void process() = 0;
};

// 遗留接口（老接口）
class IAdaptee{
public:
    virtual void foo(int data) = 0;
    virtual int bar() = 0;
};

// 遗留类型
class OldClass: public IAdaptee{
public:
    virtual void foo(int data){
        // ...
    }
    virtual int bar(){
        // ...
    }
};

// 对象适配器（推荐）
class Adapter: public ITarget{ // 继承
protected:
    IAdaptee* pAdaptee; // 组合（多态）
    
public:
    Adapter(IAdaptee* pAdaptee){
        this->pAdaptee=pAdaptee;
    }
    
    virtual void process(){
        int data=pAdaptee->bar();
        pAdaptee->foo(data);
    }
};

// 类适配器（十分不推荐）
class Adapter: public ITarget, protected OldClass{ // 多继承（无复用性，绑死OldClass）
    // ...
}

int main(){
    IAdaptee* pAdaptee = new OldClass(); // 老接口
    ITarget* pTarget = new Adapter(pAdaptee);
    pTarget->process();
}

class stack{ // STL中stack包含deque，看作是种适配器
    deqeue container;
    // ...
};

class queue{ // STL中queue包含deque，看作是种适配器
    deqeue container;
    // ...
};
阅读全文 »

发表于 更新于 本文字数： 623 阅读时长 ≈ 2 分钟

Prim：从一颗小树长大

思路和Dijkstra基本一致，唯一不同就是dist记录的是与集合的距离而非与起点的距离

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// Leetcode 1584 连接所有点的最小费用
// points = [[0,0],[2,2],[3,10],[5,2],[7,0]] 求坐标轴上这几个点的最小生成树的路径和
struct Node{ // 用来在优先队列里用
    int node;
    int dis;
    bool operator>(const Node& ano) const {
        return this->dis > ano.dis;
    }
};

class Solution {
public:
    int minCostConnectPoints(vector<vector<int>>& points) {
        int n = points.size(); // 节点数
        vector<vector<int>> graph(n, vector<int>(n, INT_MAX));
        for (int i = 0; i < n; ++i){ // 建图
            for (int j = 0; j < i; ++j){
                graph[i][j] = abs(points[i][0]-points[j][0]) + abs(points[i][1]-points[j][1]);
                graph[j][i] = graph[i][j];
            }
        }  
        priority_queue<Node, vector<Node>, greater<Node>> pq;
        vector<int> dist(n, INT_MAX);
        pq.push(Node({0, 0})); // 从0开始， 0到0的距离是0
        int ret = 0;
        while(!pq.empty()){
            Node cur = pq.top(); pq.pop();
            // 跟Dijkstra一样，但人家遇到终点直接可以break
            // 因为采用优先队列的方式，队列里会有重复，第一次接触的肯定是最优解，后面
            // 重复的都是大于最优解的，直接跳过，或者你用一个数组，存储对应节点最优dist
            // 每次存储比较取最小值，但是空间浪费太大了，不如这样好
            if(dist[cur.node] == 0) continue;
            dist[cur.node] = 0;
            ret += cur.dis;
            for(int i=0; i<n; ++i){
                if(dist[i] > graph[cur.node][i]){
                    dist[i] = graph[cur.node][i];
                    pq.push(Node({i, graph[cur.node][i]}));
                }
            }
        }
        return ret;
    }
};

Kruskal

利用并查集的思想

阅读全文 »
0%