AVL树实现
Easy SortedSet
概念
我们有一堆数据,希望能够支持快速的插入、删除、查询以及范围查询
我们都知道数组进行排序后,可以通过二分查找的方式快速定位数据,时间复杂度是$O(LogN)$,但是如果数组经常发生插入、删除操作,就需要进行大量平移,时间复杂度是$O(N)$。
那用平衡树呢?AVL树、红黑树都是经过深度优化的动态数据结构,他们的插入删除查找都可以在$O(LogN)$的时间内完成,但是他们实现起来较为复杂,且对于范围查询,还需要进行中序遍历,但至少比数组好多了。
那链表呢,链表的插入删除是很方便,但关键查询呢,它能进行二分查找吗?链表无法随机访问,怎么二分?很显然,直接对普通链表进行二分查找是困难的。1990年,Pugh发表论文《Skip Lists: A Probabilistic Alternative to Balanced Trees》,创造性的提出了自己的解决方案:”如果不能在节点间跳跃,那就建造可以跳跃的桥梁吧!”,跳跃表(SkipList)正式被提出。
跳跃表是一种概率性的有序数据结构,通过建立多级索引来加速查找,可以看作是在链表基础上加了“快速通道”,变相了实现对链表的二分查找,并且,范围查找也能够很轻易的完成,只要找到目标,就可以沿着链条依次访问。
游戏里排行榜一般是采用Redis Sorted Set,它在数据规模较大时的底层数据结构就是跳跃表+哈希表。
- 跳跃表:天然支持有序插入、删除和范围查询,时间复杂度O(log n)
- 哈希表:用于快速查找特定用户的当前位置和分数(O(1))
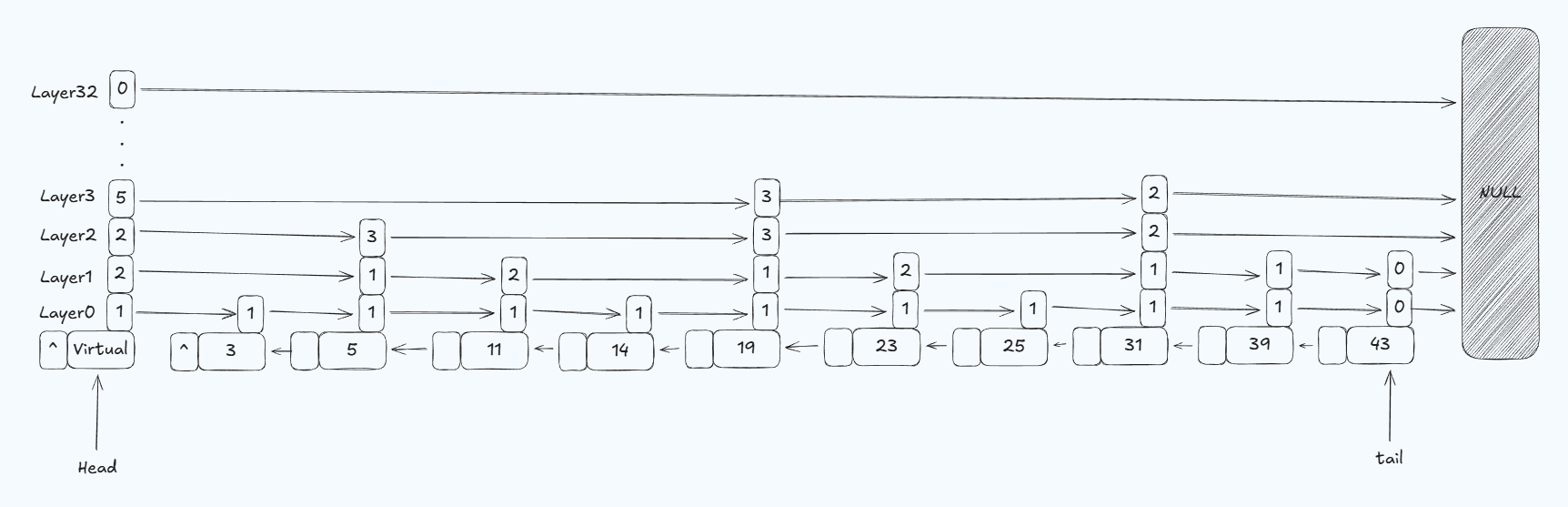 跳跃表的每个节点拥有一个前序指针和多层后继指针。每层后继指针都独立成链,每个节点在插入时,都会按照概率分配给它多少层后继指针(至少一层)。类似抛硬币,落到正面,就给它加一层后继指针,然后继续抛硬币;落到反面就结束。当然,硬币正面的概率不一定是50%(实际有论文提出,包括业内经验来看,25%的概率是对性能和内存占用权衡后的得到的较优选择)。实际上,作者最初考虑过确定性跳表,即第0层是全连接,第1层是隔1个连接,第2层是隔3个连接…但是这样会导致插入和删除需要进行大量调整,复杂度变高,从而引入随机性,不仅简化了插入和删除的操作,并且统计上仍然是接近二分的结构。
跳跃表的每个节点拥有一个前序指针和多层后继指针。每层后继指针都独立成链,每个节点在插入时,都会按照概率分配给它多少层后继指针(至少一层)。类似抛硬币,落到正面,就给它加一层后继指针,然后继续抛硬币;落到反面就结束。当然,硬币正面的概率不一定是50%(实际有论文提出,包括业内经验来看,25%的概率是对性能和内存占用权衡后的得到的较优选择)。实际上,作者最初考虑过确定性跳表,即第0层是全连接,第1层是隔1个连接,第2层是隔3个连接…但是这样会导致插入和删除需要进行大量调整,复杂度变高,从而引入随机性,不仅简化了插入和删除的操作,并且统计上仍然是接近二分的结构。
代码
YOLOv4,v5,X理解
YOLOv4
YOLOv4是在YOLOv3的基础上进行了一些改进,但是整个流程依旧是YOLOv3,比如正负样本的划分、忽略样本等等。
其中添加的改进主要有如下几点:
- 跨阶段局部网络(Cross-Stage-Partial, CSP)作为主干网络进行特征提取
- Mish激活函数(backbone)和Leaky ReLU(neck)
- Mosaic数据增强、MixUP数据增强
- 添加注意力机制模块
- CIoU作为边框回归损失
- 在neck中添加空间金字塔池化(Spatial Pyramid Pooling, SPP)提升感受野
- 在原先YOLOv3 neck的特征金字塔网络(Feature Pyramid Netword, FPN)的基础上改进为路径聚合网络(Path Aggregation Network, PAN)
YOLOv5
YOLOv5并无论文,我以开源代码中的实现来说明(version 5.0)。
YOLOv3源码理解
0 主干网络
YOLOv3采用DarkNet-53网络,结构如下图(DarkNet-53预训练于ImageNet,由于是1000类的分类,所以网络最后输出经过全连接层。但是目标检测不需要那个全连接层,因此实际上只使用了“DarkNet-52”,共52层卷积层):
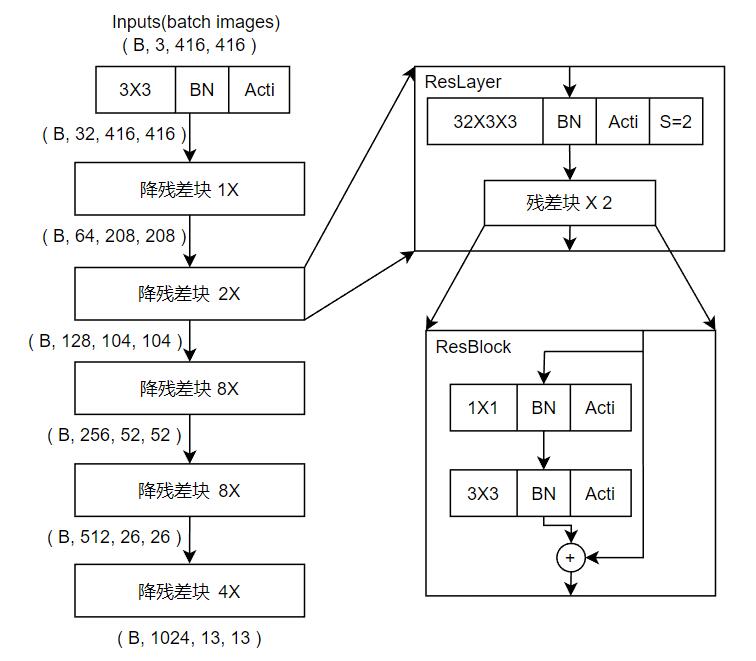
- BN为批归一化层,Acti为激活函数,YOLOv3采用LeakyReLU
- 输入批次经过一个3X3卷积改变通道数为32,然后经过5个降残差块。每个降残差块包含一次步幅为2的3X3卷积加上一系列残差块。每个残差块包含一次1X1卷积降低通道数,再经过一次3X3卷积提升通道数,最后和残差边进行连接。
- 整体主干网络清晰,每经过一个降残差块,通道数翻倍,特征图宽高减半。
1 预测分支网络
C与CPP互相调用
0. 说明
- C++采用g++编译,C采用gcc编译。两者主要不同点是:C++编译考虑到函数重载,会将原函数“改名”(命名倾轧name mangling);而在C中不存在重载,函数名不会变动。
- g++和gcc可以兼容C++和C的编译方式,但是默认情况下g++采用C++编译方式;而gcc采用C的编译方式
- 注意:gcc编译C++文件时不会主动链接C++用到的库stdc++,需要手动指定链接选项
-lstdc++ __cplusplus宏定义会在编译cpp文件以及用C++的方式编译时被包含,因此用gcc编译.cpp文件或者g++编译.c、.cpp文件都会有这个宏- 之所以用条件判断,因为gcc不认识
extern "C",直接编译会报错
1. C++调用C
只需要声明时包含extern "C"即可。下面的代码中,func.h可以不动,在main.cpp调用时,直接extern "C" int func(int, int)也是可以的。只需要让编译器按照C的方式编译,不要改动函数名即可正确链接的函数符号。
1 | // func.h 不论.c还是.cpp文件调用,都不会出错 |
Qt信号与槽
Qt的信号与槽机制是如何实现的?
猜测1:回调函数
- 这里用C11出现的function来封装所有可调用的对象:函数、指针、lambda、bind创建的对象、重载了小括号的仿函数
- 通过unordered_multimap来记录某个字符串与一个可调用对象的映射(注意unordered_multimap未实现[]和at函数,不能通过这类方式获取value)
1 | class Connection { |
输出结果:
拓扑排序和二分图
1 拓扑排序(有向图)
课程表Ⅱ
1.1 BFS(易理解)
创建一个表示入度的数组,初始将入度为0的节点加入队列,后续依次弹出队列,每次弹出node,减小node指向的节点的入度,入度为0的加入队列,直到队列为空,结果需要判定出队列的节点数和图的总节点数相同,不同则代表有循环
1 | class Solution { |
带限制的最短路
错误示例(Dijkstra)
全局的dist记录着最短距离,但它并未记录是几跳获得的。例如,到达终点的前一跳,从X->dst,我的代码中只限制了到达X最多k+1跳,此时更新了dist[X],当更新到dst时,利用的dist[X]是经过k跳的X作为跳板,则结果是经过了k+2跳,超出了限制,因此结果必然是错误的。
1 | class Item { |